欧拉线定理

欧拉线定理

欧拉线定理：三角形的外心、垂心和重心在一条直线上,而且外心和重心的距离是垂心和重心的距离一半。

证明：

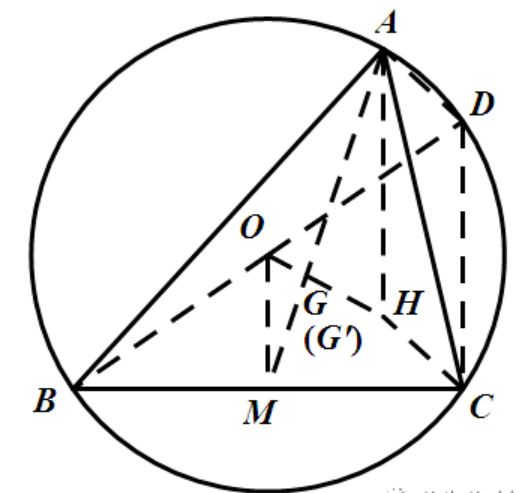
如图，三角形ABC，HGO分别是其垂心，重心和外心，连接BO并延长，和外接圆O相交于D，连接AH，AD，CD和CH。

因为BD为外接圆O的直径枯汪，所以CD垂直BC，AD垂直AB；

又H为垂心，所以AH垂直BC，CH垂直AB；

因此CD//AH，HC//AD，ADCH为平行四边形，AH = DC；

又O，M分别为BD和没裤仔BC中点，OM为三角形纯唤DBC的中位线，OM = DC / 2 = AH / 2；

连接AM，OM，OH，OH交AM于G'；显然，三角形AHG'相似于三角形MOG'，且对应边的比为AH / OM = 2，因此AG' = 2G'M，由于重心是中线靠近边的三等分点，因此重心G和G'重合，因此OGH三点共线。