摆线形是什么形状？

摆线形是什么形状？

如下图：

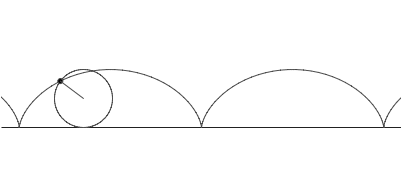
摆线是一个圆沿一条直线运动时，圆边界上一定点所形成的轨迹。它是一般旋轮线的一种。

圆上定点的初始位置为坐没桐标原点，定直线为x轴。当圆核察拍滚动j 角以后，圆上定点从 O 点位置到达P点位置。当圆滚动一周，即 j从O变动2π时，动圆上定点描画出摆线的第一拱。再向前滚动一周， 动圆上定点描画出第二拱，继续滚动，可得第三拱，第四拱……，所有这些拱的形状都是完全相同的 ，每一拱的拱高为2a（即圆的直径），拱宽为2πa（即圆的周长）。

性质：

1、它的长度等于旋转圆直径的 4 倍。尤为令人感兴趣的是，它的长度是 一个不依赖于π的有理数。

2、在弧线下的面积，是旋转圆面积的三倍。

3、圆上描出摆线的那个点，具有不同的速度——事实上，在特定的地方它改羡甚至是静止的。

4、当弹子从一个摆线形状的容器的不同点放开时，它们会同时到达底部。

公式：

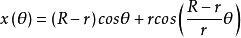
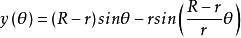
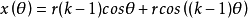
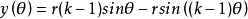
如果k是整数，那么曲线是闭合的，并且曲线有k个尖峰（即尖角，曲线不可微分）。特别地，对于k = 2，曲线是直线，圆圈称为卡尔达诺圆。卡尔达诺圆是第一个描述内摆线及其在高速印刷中的应用。

参考资料来源：百度百科——摆线