椭圆的参数方程（焦点在Y轴上）的推导

椭圆的参数方程（焦点在Y轴上）的推导

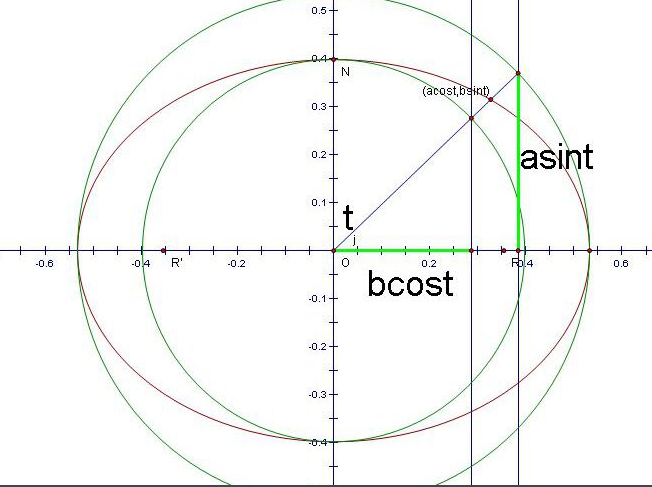
参数方程的原理（改宏X轴的）：设A为椭圆上一点：坐标(X，Y)。O=(-c，0)。O为椭圆焦点K是以OX为始边OA为终边的角，取K为参数，X=|OA|COS(K)，Y=|OB|SIN(K)，设参数方程为X=aCOS(K)Y=bSIN(K)。

==>X^2/a^2+Y^2/b^2=(COSK)^2+(SINK)^2=1为椭圆标准方程。==>参数方程X=aCOS(K)Y=bSIN(K)为椭圆的参数方程。

扩展资料：

（1）曲线的极坐标参数方程ρ=f(t)，θ=g(t)；

（2）圆的参数方程 x=a+r cosθ y=b+r sinθ（θ∈ [0，2π) ） (a,b) 为拆旅圆心坐标，r 为圆半径，θ 为参数，(x,y) 为经过点的坐标；

（3）椭圆的参数方程 x=a cosθ　 y=b sinθ（θ∈[0，2π）） a为长半轴长 b为短半轴长 θ为参数 

（4）双曲线的参数方程 x=a secθ （正割） y=b tanθ a为实半轴长 b为虚半轴长 θ为参数；

（5）抛物线的参数方程 x=2pt^2 y=2pt p表示焦点核御册到准线的距离 t为参数。