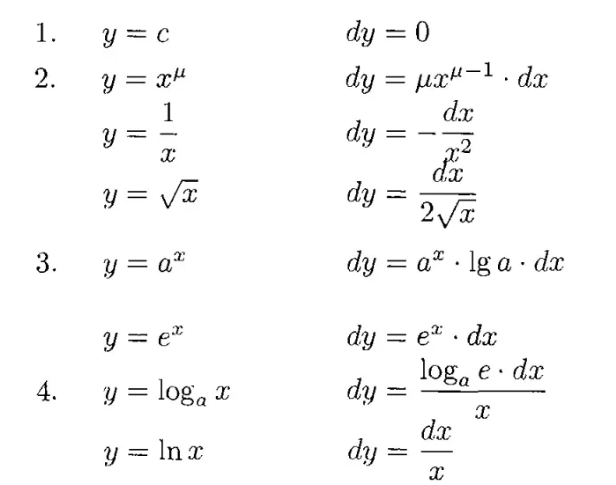全微分基本公式是什么dz?

全微分基本公式是什么dz?

全微分基本公式是dz=z'(x)dx+z'(y)dy。如果函数z=f(x，y)在(x，y)处的烂档全增量Δz=f(x+Δx，y+Δy)-f(x，y)可以表示为Δz=AΔx+BΔy+o(ρ)，其中A、B不依赖于Δx，Δy，仅与x，y有关，ρ趋近于0(ρ=√[(Δx)2+(Δy)2])。

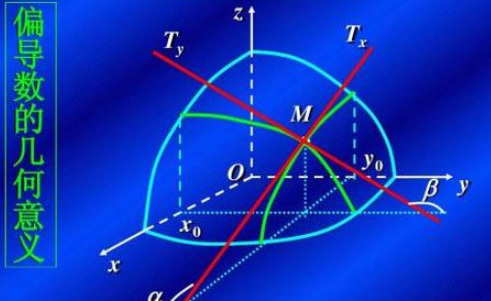
全微分定义

全微分是微积分学的一个概念，指多元函数的全增量的线性主部，一个多元函数在某点的全微分存在的充分条件是此函数在该点某邻域内的各个偏导数存在且皮虚偏导函数在该点都连续，则此函数在该点可微，存在条件全微分继承了部分一元函数饥握乱实函数的微分所具有的性质。

但两者间也存在差异，从全微分的定义出发，可以得出有关全微分存在条件的多个定理，充分条件一个多元函数在某点的全微分存在的充分条件是，此函数在该点某邻域内的各个偏导数存在且偏导函数在该点都连续。