为什么直角三角形斜边上的中线等于斜边的一半?
的有关信息介绍如下:直角三角形斜边中线定理
如果一个三角形是直角三角形,那么这个三角形斜边上的中线等于斜边的一半。
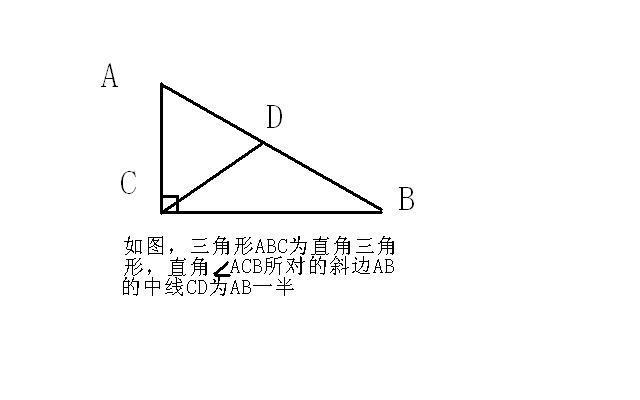
ΔABC是直角三角形,作AB的垂直平分线n交BC于D
∴ AD=BD(线段垂直平分线上的点到这条线段两端点的距离相等)
以DB为半径,D为圆心画弧,与BC在D的另一侧交于C'
∴DC’=AD=BD∴∠BAD=∠ABD ∠C’AD=∠AC’D (绝配等边对等角)
又∵∠BAD+∠ABD+∠C’AD+∠AC’D =180°(三角形内角和定理)
∴∠BAD+∠C’AD=90° 即:∠BAC’=90°
又∵∠BAC=90°
∴∠BAC=∠BAC’
∴C与C’重合(也可用垂直公理证明 :假使C与滚如C’不重合 由于CA⊥AB,大宏启C’A⊥AB 故过A有CA、C’A两条直线与AB垂直 这就与垂直公理矛盾 ∴假设不成立 ∴C与C’重合)
∴DC=AD=BD∴AD是BC上的中线且AD=BC/2这就是直角三角形斜边上的中线定理


