狗追兔子的问题

狗追兔子的问题

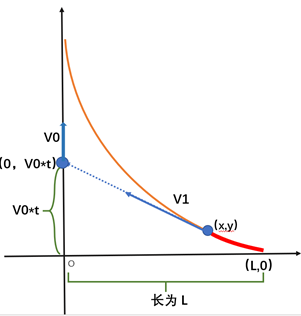
假设速度为v1的猎狗，从(L,0)出发（这里的L即为题目给的s，v1为题目的v2，v0为题目的v1），t时刻对应坐标（x,y）。

由于t=0时兔子和猎狗同时出发，所以兔子坐标为（0，v0*t）。

狗的速度方向指向兔子，所以狗和兔子的连线对任意时刻t而言，都是运动轨迹在（x，y）的切线。

于是由几何关茄凯系可知

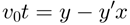
图中涂红的一段是猎狗走过的路程

所以，由曲线长度公式得

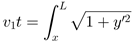
令

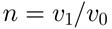
 n∈(1,+∞)

由以上三式得

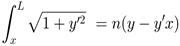
两边同时微分得

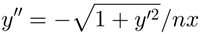
以上式子再加上x=L，y’=0的初始条件，可以解出狗追兔子曲线。　至于具体怎么解，楼主可以琢磨一下。其轨迹方程为 

令x=0，则y、t都可以解得

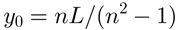
y0为最终追上时，兔子的纵坐标

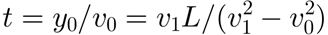
t为追及时间

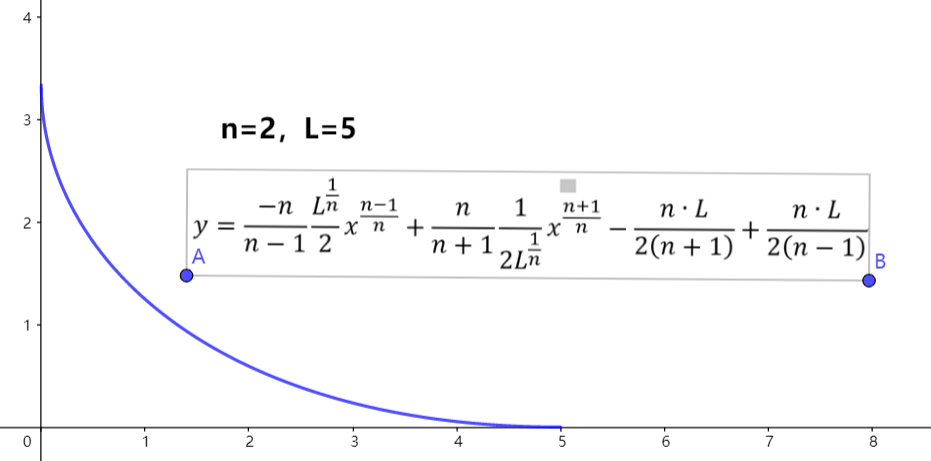
画出大致的图像，比如n=2，L=5

当然，以上是高肢族数的解法，如果题主是在物理竞赛书上看到这题，建议使用物理解颤饥唤法。

希望能帮到您，谢谢！