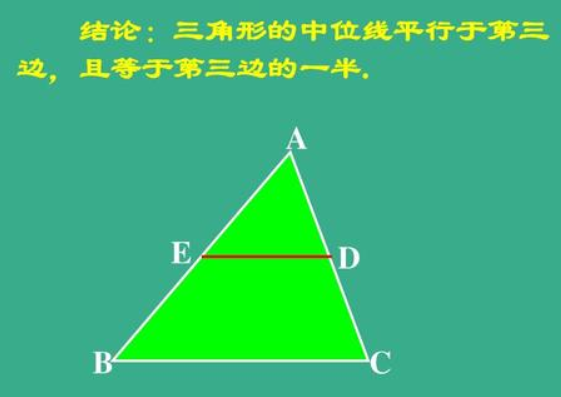
三角形中位线逆定理

三角形中位线逆定理

三角形中位线逆定理主要有两个，不同的逆定理有不同的证明方法。

一、逆定理一：在三角形内，与三角形的两边相交，平行且等于三角形第三边一半的线段是三角形的中位线 。

DE//BC，DE=BC/2，则D是AB的中点，E是AC的中点。

证明：∵DE∥BC

1、∴△ADE∽△ABC，

2、∴AD:AB=AE:AC=DE:BC=1:2，

3、∴AD=AB/2，AE=AC/2，即D是AB中点，E是AC中点。

二、逆定理二：在三角形内，经过三角形一边的中点，且与另一边平行的线段，是三角形的中位线 。

D是AB的中点，DE//BC，则E是AC的中点，DE=BC/2，

证明：取AC中点E'，连接仔缺扒DE'，则有AD=BD，AE'=CE'，

1、∴DE'是三角形ABC的中位线，

2、∴DE'∥BC，

又∵DE∥BC，

3、∴DE和DE'重合（过扮碰直线外一点，有且只有一条直线与已知直线平行），

4、∴E是中点，DE=BC/2。

扩展资料：

三角形中位线逆定理的注意事念昌项：

在三角形内部，经过一边中点，且等于第三边一半的线段不一定是三角形的中位线。因为在△ABC中，D是AB中点，E在AC上，DE=BC/2，那么DE不一定是△ABC的中位线。理由如下：

1、以D为圆心，DE为半径作圆，设⊙D与AC交于另一点E'，则有DE'=DE=BC/2，但DE'不是三角形的中位线。

2、但在一定条件下该命题是真命题。根据正弦定理解三角形可知，若∠A是锐角，当DE≥AD（即当BC≥AB），或DE=ADsinA（即BC=ABsinA，此时∠C=90°）时，命题成立。若∠A是钝角或直角，则当DE>AD（即BC>AB）时，命题成立。

参考资料来源：百度百科-三角形中位线定理