Simone两直线垂直斜率关系证明
的有关信息介绍如下：证明如下：
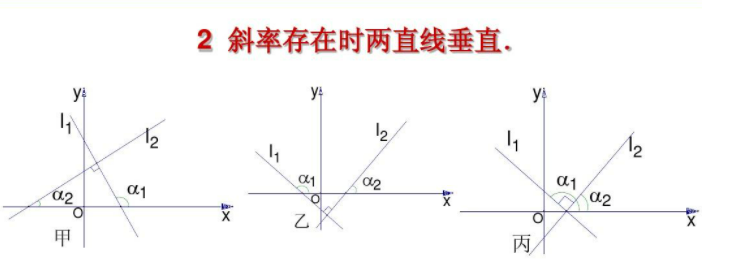
设两条直线的斜率为k1,k2,倾斜角为a,b。
如果梁返两条直线垂直,那么它们之间的夹角为90度。
所以tan(a-b)=tan90=(tana-tanb)/(1+tanatanb)=无穷大。
因为漏简tana=k1,tanb=k2。
所以1+tanatanb=1+k1k2=0。
因此k1k2=-1。
方法二：
设一条直线的斜率是tana,另一条是tanb，两条线的夹角为返渣裤b-a。
tan(b-a)=[tanb-tana]/[1+tana tanb]。
如果 1 + tana tanb = 0,即 tana tanb = -1。
那么 b - a = 90度。
所以,结论是：两条直线如果互相垂直,则两直线的斜率之积为-1。
