什么是范德蒙德行列式？其形式怎样的？

什么是范德蒙德行列式？其形式怎样的？

题主想说的应该是范德蒙行列式。

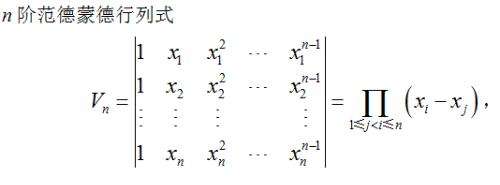
范德蒙行列式很好区分，它有一个典型的形式：

一个n阶范德蒙行列式，

第一行全是1，有n个1，

第二行是X1,X2,X3,...,Xn，

第三行是X1²,X2²,X3²,...,Xn²，

以此类推，

第n行是X1ⁿ,X2ⁿ,X3ⁿ,...,Xnⁿ。

又因为经过转置行列式的值不变，所以范德蒙行列式还有一种行列式，如图：

计算n阶范德蒙行搜念列式的值，用世笑困数学归升枝纳法。

当n=2时，范德蒙德行列式D2=x2-x1，范德蒙德行列式成立。

现假设范德蒙德行列式对n-1阶也成立，对于n阶有: 首先要把Dn降阶，从第n列起用后一列减去前一列的x1倍，然后按第一行进行展开，就有Dn=(x2-x1)(x3-x1)...(xn-x1)Dn-1，于是就有Dn=∏ (xi-xj)(其中∏ 表示连乘符号，其下标i,j的取值为m≥i>j≥1)，原命题得证。