高中数学：等差数列前N项和公式

高中数学：等差数列前N项和公式

等差数列前N项和公式为：Sn=n(a1+an)/2或Sn=na1+n(n-1)d/2=dn^2/2+(a1-d/2)n

方法是倒序相加

Sn=1+2+3+……+(n-1)+n

Sn=n+(n-1)+(n-2)+…敬纤…+2+1

两式相加

2Sn=(1+n)+(2+n-1)+(3+n-2)+……+(n-1+2)+(n+1)=(n+1)+(n+1)+(n+1)+…野渗…+(n+1)+(n+1)

一共n项(n+1)

2Sn=n(n+1)

Sn=n(n+1)/2

等差数列的判定

满足以下条件｛an｝即为等差数列

（1）

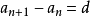
(d为常数、n ∈N*) 

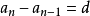
n ∈N*，n ≥2，d是常数

（2）

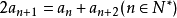
（3）

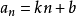
k、b为常颂稿脊数,n∈N*

（4）

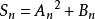
A、B为常数，A不为0，n ∈N* 

参考资料来源：百度百科-等差数列