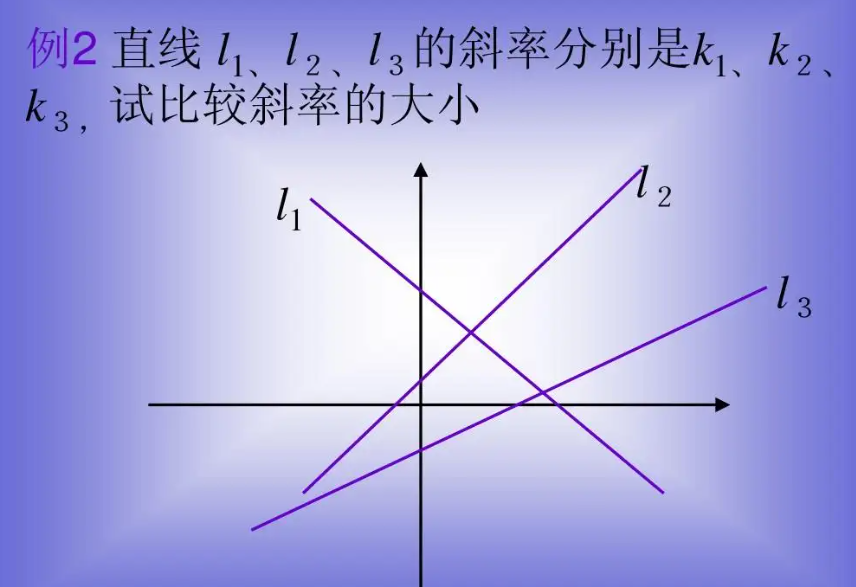
斜率怎么求?
的有关信息介绍如下:对于过两个已知点(x1,y1) 和 (x2,y2)的直线,若x1≠x2,则该直线的斜率为k=(y1-y2)/(x1-x2)。
斜率表示一条直线(或曲线的切线)关于(横)坐标轴倾斜程度的量。它通常用直线(或曲线的切线)与(横)坐标轴夹角的正切,或两点的纵坐标之差与横坐标之差的比来表示。又称“角系数”,是一条直线对于横晌桥坐标轴正向夹角的正切,反映直线对水平面的倾斜度。
扩展资料:
斜率的不同分类:
1、“斜率”就是“倾斜的程度”。斜坡上两点A,B间的垂直距离h(铅直高度)与水平距离l(水平宽度)的纳谨颂比叫做坡度(或叫做坡比),用字母i表示,通常坡度i用分子为1的分数来表示。
2、解析几何中,要通过点的坐标和直线方程来研究直线通过坐标计算求得,使方程形式上较为简单。如果只用倾斜角一个概念,那么它在实际上相当于反正切函数值arctank,难于直接通过坐标计算求得,并使方程形式变得复杂。
3、坐标平面内,每一条直线都有唯一的倾斜角,但不是每一条直线都有斜率,倾斜角是90°的直线(即x轴的垂线)没有斜率。在今后洞郑的学习中,经常要对直线是否有斜率分情况进行讨论。
参考资料来源:百度百科—斜率