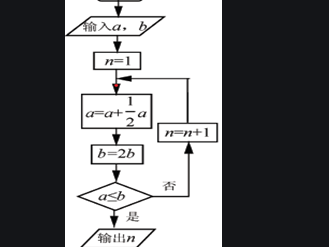
ln2等于多少用e表示?
的有关信息介绍如下:ln2=loge2,就是以e为底2的对数loge2的简写形式,其中e=2.71828···属无理数,如果设x=ln2则e^x=(2.71828···)^x=2,x=ln2介于1/2和1之间。
相关介绍:
将对数加以改造使之广泛流传的是纳皮尔的朋友布里格斯(H.Briggs,1561-1631),他通过研究《奇妙的对数定律说明书》,感到其中的对数用起来很不方便,于是与纳皮尔商定,使1的对数为0,10的对数为1,这样饥喊就得到了现在所用的以10为底的常用对数。
由于我们的数系是十进制,因此它在数值上计算具有优越性。1624年,布里格斯出版了《对数算术》,公布了以10为底包含1~20000及90000~100000的14位常用对数表。
根据对数运算原理,人们还发明了对数计算尺。300多年来,对数计算尺一直是科学工作者,特别是工程技术人员必备的计算工具,直到20世纪70年代才让位给电子计算器。尽管作为一种计算工具,对数计算尺、对数表都不再重要了,但是,对数的思想方法却仍然具有生命力。
从对数的发明过程我们可以发现,纳皮尔在讨论对数概念时,并没有使用指数与对数的互逆关系,造成这种状况的主要原因是当时还没有明确的指数概念,就连指数符号也是在20多年后的1637年才由法国数学家笛卡儿(R.Descartes,纳数1596-1650)开始使用。
直到18世纪,才由瑞士数学家欧拉发现了指数与对数的互逆关系。在1770年出版的一部著作中,欧拉首先使用y=a^x(a>0,且a≠1)来定义x=log (a) y (a>0,且a≠1),他指出:"对数源于指数"。对数的发明先于指数,成为数学史上的珍闻。洞肢首


