什么是不等式与不等式组?

什么是不等式与不等式组?

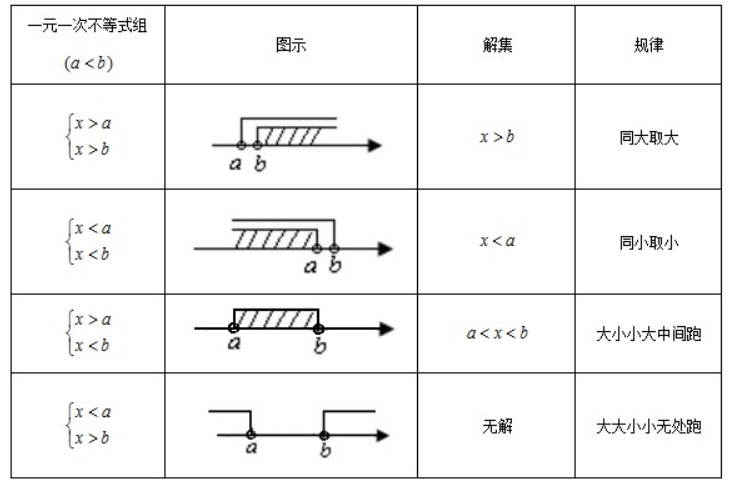
不等式组 几个含有相同未知数的不等式联立起来，叫做不等式组不等式 用不等号将两个解析式连结起来所成的式子。例如x2＋y2≥2xy，sinx≤1，ex＞0 ，2x＜3等 。根据解析坦竖伏式的分类也可对不等式分类，不等号两边的解析式都是代数式的不等式，称为代数不等式；只要有一边是超越式，就称为超越不等式。例如lg(1＋x)＞x是超越不等式。不等式和方程一样，也是代数里的一种重要模型．在概念方面，它与方程很类似，尤其重要的是不等式具有一系列基本性质，而且“数学的基本结果往往是一些不等式而不是等式”．本讲是系统学习不等式的基础． 下面先介绍有关一次不等式的基本知识，然后进行例题分析． 1．不等式的基本性质这里特别要强调的是在用一个不等于零的数或式子去乘(或去除)不等式时，一定要注意它与等式的类似性质上的差异，即当所乘(或除)的数或式子大于零时，不等号方向不变(性质(5))；当所乘(或除)的数或式子小于零时，不等号方向要改变(性质(6))． 2．区间概念 在许多情况下，可以用不等式表示数集和点集．如果设a，b为实数，且a＜b，那么 (1)满足不等式a＜x＜b的数x的全体叫作一个开区间，记作(a，b)．如图1－4(a)． (2)满足不等式a≤x≤b的数x的全体叫作一个闭区间，记作[a，b]．如图1－4(b)． (3)满足不等式a＜x≤b(或a≤x＜b)的x的全体叫作一个半开半闭区间，记作(a，b](或[a，b))．如图1－4(c)，(d)．3．一次不等式的一般解法 一元一次不等式像方程一样，经过移项、合并同类项、整理后，总可以写成下面的标准型：ax＞b，或ax＜b．为确定起见，下面仅讨论前一种形式． 一元一次不等式ax＞b．(3)当a=0时，用区间表示为(-∞，+∞)． 例1 解不等式解 两边同时乘以6得12(x+1)+2(x-2)≥21x-6，化简得-7x≥-14， 两边同除以-7，有x≤2．所以不等式的解为x≤2，用区间表示为(-∞，2]． 例2 求不等式的正整数解．正整数解，所以原不等式的正整数解为x=1，2，3． 例3 解不等式分析与解 因y2+1＞0，所以根据不等式的基本性质有例4 解不等式为x+2＞7，解为x＞5．这种错误没有考虑到使原不等式有意义的条件：x≠6． 解 将原不等式变形为解之得所以原不等式的解为x＞5且x≠6． 例5 已知2(x-2)-3(4x-1)=9(1-x)，且y＜x+9，试让携比较 解 首先解关于x的方程得x=-10．将x=-10代入不等式得y＜-10+9，即y＜-1．例6 解关于x的不等式：解 显然a≠0，将原不等式变形为3x+3-2a2＞a-2ax， 即(3+2a)x＞(2a+3)(a-1)．说明 对含有字母系数的不等式的解，也要分情况讨论． 例7 已知a，b为实数，若不等式(2a-b)x+3a-4b＜0解 由(2a-b)x+3a-4b＜0得(2a-b)x＜4b-3a．由②可求得将③代入①得所以b＜0．于是不等式(a-4b)x+2a-3b＞0可变形为因为b＜0，所以下面举例说明不等式组的解法． 不等式组的解是不等式组中所有不等式解的公共部分． 若不等式组由两个不等式组成，分别解出每一个不等式，其解总可以归纳成以下四种情况之一(不妨设α＜β)：解分别为：x＞β；x＜α；α＜x＜β；无解．如图1－5(a)，纤银(b)，(c)，(d)所示．若不等式组由两个以上不等式组成，其解可由下面两种方法求得： (1)转化为求两两不等式解的公共部分．如求解(2)不等式组的解一般是个区间，求解的关键是确定区间的上界与下界，如求解确定上界：由x＜4，x＜8，x＜5，x＜2，从4，8，5，2这四个数中选最小的数作为上界，即x＜2． 确定下界：由x＞-4，x＞-6，x＞0，x＞-3．从-4，-6，0，-3中选最大的数作为下界，即x＞0． 确定好上、下界后，则原不等式组的解为：0＜x＜2．不等式组中不等式的个数越多，(2)越有优越性． 例8 解不等式组解 原不等式组可化为解之得例9 解关于x的不等式组解 解①得4mx＜11，③ 解②得 3mx＞8． ④ (1)当m=0时，③，④变为原不等式组无解． (2)当m＞0时，③，④变形为(3)当m＜0时，由③，④得练习六1．解下列不等式或不等式组：2．解下列关于x的不等式或不等式组：