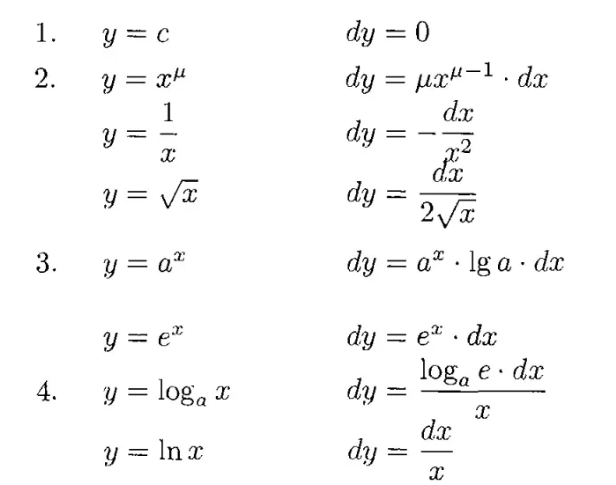什么是微分,什么是全微分,他们的区别是什么
的有关信息介绍如下:
高等数学中,将为分放在了第一册,和导数放到一起,而全微分好像是在第二册.什么是微分?首先得从导数说起.一次导数,就是求变化速度的问题,用来求解变化速度的快慢,从几何意义上讲就是斜率的问题猛基御,是微分的基础.从表面上看,微分与导数的区别不大,因为我们平时在求微分的时候,运用的也是枝岩导数的基本公式,我们能看到的也只是锋盯表示上的区别,导数用f'(x)表示,而微分用dy表示.要找出区别,还得从几何意义上来考虑.一条直角坐标系中的曲线,某一点的导数代表的是曲线在这一点的斜率,而微分则表示在这一点处的一个无穷小量,这个无穷小量就是这一点处的函数值,即f(x),减去此处的斜率与一个很小的det(x)的乘积,用数学表达式来表示就是:dy=f(x.)-f'(x)dx .说的简单一点就是:导数代表斜率,微分代表真实值与用导数近似之后的差值,是一个无穷小量.图形你可以自己画一下,或者你的课本上也应该有,这是一个难点,也是关系到后面的知识的问题. 下面说一下全微分.在微分的学习中,我们接触的只是对一元一次方程或者是一元高次方程的求导,也就是说,函数值y只与变量x有关系.学到后面,我们接触到了多元方程,函数值不仅仅与x有关,还与其他变量有关,例如:f(x)=3x-5y+7z.这样,微分的概念在这里就变得模糊了,因为要表达函数值的变化情况,单单求其中一个变量已经不够了.于是引进了偏微分与全微分的概念.偏微分表示函数值在某“一个”方向上的变化情况,只需对其中的一个变量求微分即可;而全微分则是表示函数值对所有的变量的变化情况,需要对所有的变量求微分.具体到求解的方法,你学到那里就自然明白了. 总结:导数是微分的基础,微分是全微分的基础,微分只能解决一元函数的问题,是应用在二维坐标系的工具,全微分解决二元以及高元函数的问题,应用于三维以及高维坐标空间.数学本来就是一门很抽象的学问,单凭我这么说,你也未必能看得很明白,多做一些这方面的题就会有更深层次的了解了,书读百遍,其义自现嘛!