Simone数学中π等于多少
的有关信息介绍如下：π是一个无理数，所以不能直接表示出来。
圆周率（π）：3.14159 26535 89793 23846 2643383279 50288 41971 69399 37510 58209 74944 59230 78164 06286 20899 86280 34825 34211 70679 82148 08651 32823 06647 09384 46095 50582 23172 53594 08128 48111 74502 84102 70193 85211.........（约等于3.141592654），通常用3.14来表示π的数值。
而用十位小数3.141592654便足以应付一般计算。即使是工程师或物理学家要进行较精密的计算，充其量也只需取值至小数点后几百个位。
圆周率（ 
）一般定义为一个圆形的猛亏周长（ 
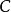）与直径（ 
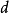）之比：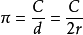 
，或直接定义为单位圆的周长的一半。由相似图形的性质可知，对于任何圆形，
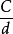的值都是一样，这样就定义出常数
。
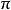扩展资料
古希腊作为古代几何王国对圆周率的贡献尤为突出。古希腊大数学家阿基米德(公元前287–212 年) 开创了人类历史上通过理论计算圆周率近似值的先河。阿基米德从单位圆出发，先用内接正六边形求出圆周率的下界为3，再用外接正六边形并借助勾股定理求出圆周率的上界小于4。
接着，他对枝前神内接正六边形和外接正六边形的边数分别加倍，将它们分别变成内接正12边形和外接正12边形，再借助勾股定理改进圆周率的下界和上界。他逐步对内接正多边形和悔哗外接正多边形的边数加倍，直到内接正96边形和外接正96边形为止。
最后，他求出圆周率的下界和上界分别为223/71 和22/7， 并取它们的平均值3.141851 为圆周率的近似值。阿基米德用到了迭代算法和两侧数值逼近的概念，称得上是“计算数学”的鼻祖。
参考资料：百度百科——π
