奇函数乘奇函数

奇函数乘奇函数

函数与奇函数的乘积是偶函数。

奇函数乘奇函数的奇偶性判断：

设y=f(x)是定义域A上的奇配迹哪函数，y=g(x)是定培码义域B上的奇函数。

因为y=f(x)的定义域A，与y=g(x)的定义域B都关于原点对称，所以这两个定义域的交集C=A∩B仍关于原点对称。

对于定义域C中的任意x，都有f(-x)g(-x)=[-f(x)]·[-g(x)]=f(x)g(x)，根据偶函数的定义可知，f(x)g(x)为偶函数。

所以，奇函数与奇函数的乘积为偶函数。

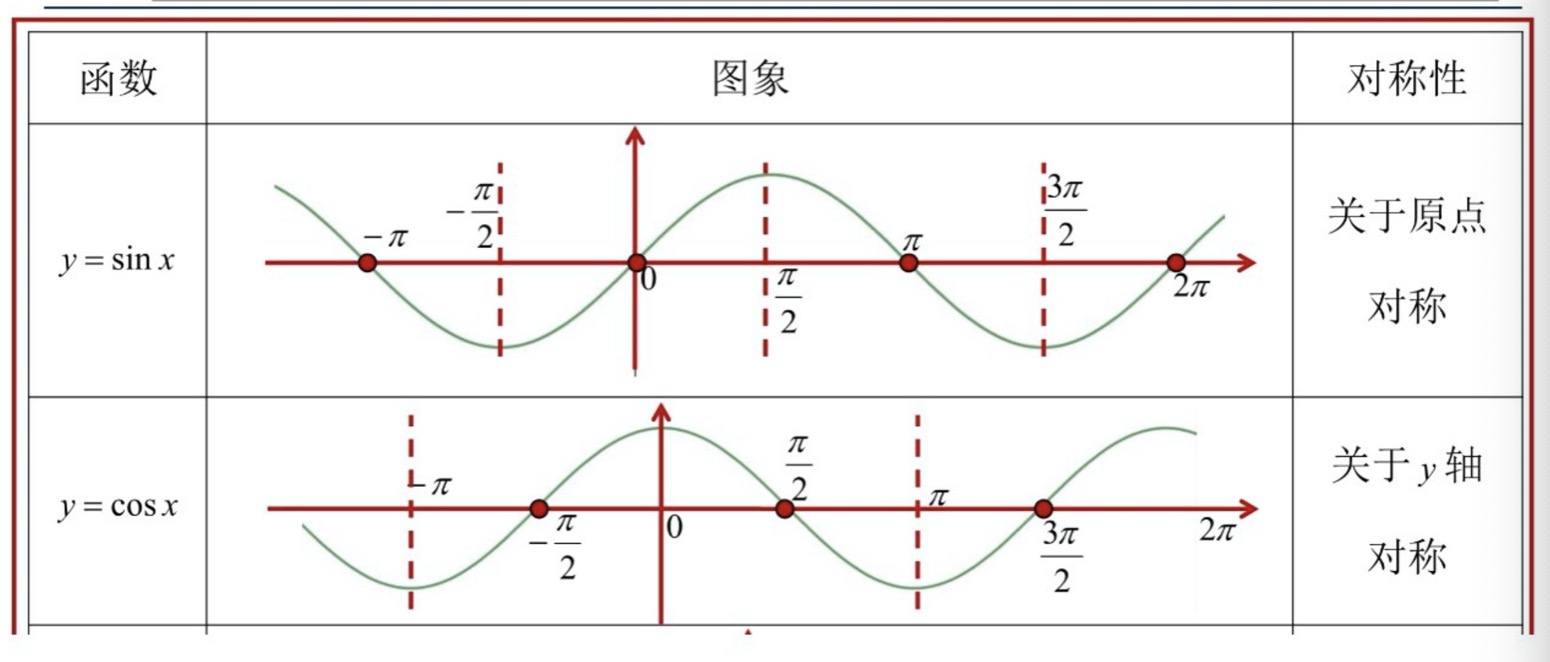
积函数的特点：

两个奇函数相加所得的和或相减所得的差为奇函数。一个偶函数与一个奇函数相州棚加所得的和或相减所得的差为非奇非偶函数。

两个奇函数相乘所得的积或相除所得的商为偶函数。一个偶函数与一个奇函数相乘所得的积或相除所得的商为奇函数。