Simone等价无穷小的定义！同阶无穷小的定义！等价无穷小和同阶无穷小的区别！
的有关信息介绍如下：1、定义
等价无穷知茄配小：是无穷小的一种。在同一点搭指上，这两个无穷小之比的极限为1，称这两个无穷小是等价的。
同阶无穷小：如果lim F(x)=0，lim G(x)=0，且lim F(x)/G(x)=c，c为常数并且c≠0，则称F(x)和 G(x)是同阶无穷小。同阶无穷小量，其主要对于两个无穷小量的比较而言，意思是两种趋近于0的速度相仿。
2、判断
等价无纳旦穷小的两个无穷小之比必须是1；
同阶无穷小的两个无穷小之比是个不为0的常数。因此，同阶无穷小中包含等价无穷小。
扩展资料：
常用的的等价无穷小公式：
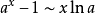
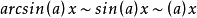
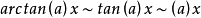
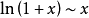
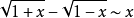
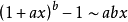
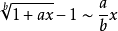
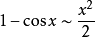
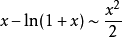参考资料来源：百度百科-等价无穷小
参考资料来源：百度百科-同阶无穷小
